Conditional Analytic Monte Carlo Pricing Scheme
Fries, Christian P.; Mark, Joshi S.: Conditional Analytic Monte Carlo Pricing Scheme for Auto-Callable Products. 2008.
Abstract
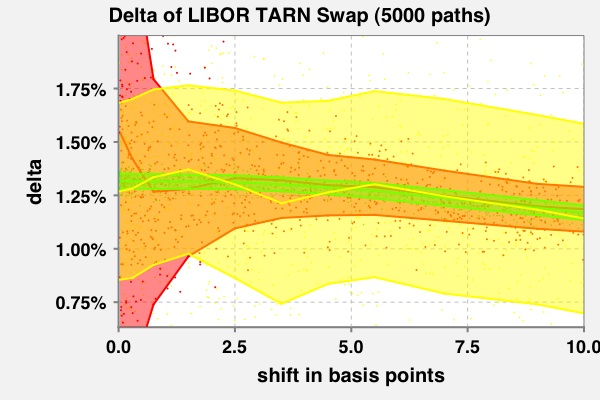
The delta of a target redemption note swap (with reverse floating index) having a short time to next reset being 0.05 (i.e., 2 1/2 weeks) with an approximate 50:50 chance of knock out. The delta is evaluated by finite differences applied to standard Monte-Carlo simulation (red), finite differences (!) applied to a partial proxy scheme simulation (yellow) and finite differences applied to a conditional analytic pricing scheme. The Monte-Carlo error of the direct simulation (red transparent corridor) explodes for small shift sizes. The Monte-Carlo error of the partial proxy simulation scheme (yellow transparent corridor) remains stable for small shift sizes, but is overall very large (due to the short time to next reset). The Monte Carlo error of the conditional analytic scheme (green transparent corridor) does not exhibit any of these defects.
In this paper we present a generic method for the Monte-Carlo pricing of (generalized) auto-callable products (aka. trigger products), i.e., products for which the payout function features a discontinuity with a (possibly) stochastic location (the trigger) and value (the payout).
The Monte-Carlo pricing of the products with discontinuous payout is know to come with a high Monte-Carlo error. The numerical calculation of sensitivities (i.e., partial derivatives) of such prices by finite differences gives very noisy results, since the Monte-Carlo approximation (being a finite sum of discontinuous functions) is not smooth. Additionally, the Monte-Carlo error of the finite-difference approximation explodes as the shift size tends to zero.
Our method combines a product specific modification of the underlying numerical scheme, which is to some extent similar to an importance sampling and/or partial proxy simulation scheme and a reformulation of the payoff function into an equivalent smooth payout.
From the financial product we merely require that hitting of the stochastic trigger will result in an conditionally analytic value. Many complex derivatives can be written in this form. A class of products where this property is usually encountered are the so called auto-callables, where a trigger hit results in cancellation of all future payments except for one redemption payment, which can be valued analytically, conditionally on the trigger hit.
From the model we require that its numerical implementation allows for a calculation of the transition probability of survival (i.e., non-trigger hit). Many models allows this, e.g., Euler schemes of Itô processes, where the trigger is a model primitive.
The method presented is effective across a large range of cases where other methods fail, e.g. small finite difference shift sizes or short time to trigger reset (approaching maturity); this means that a practitioner can use this method and be confident that it will work consistently.
Download