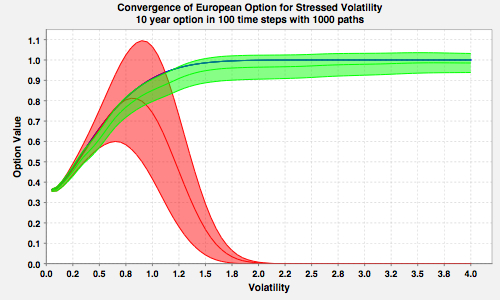
 The Monte-Carlo valuation (line) and its error estimate (corridor) for a European call option: Standard Monte-Carlo valuation (red), Monte-Carlo valuation with linear boundary condition (green) and analytic benchmark (blue).
The Monte-Carlo valuation (line) and its error estimate (corridor) for a European call option: Standard Monte-Carlo valuation (red), Monte-Carlo valuation with linear boundary condition (green) and analytic benchmark (blue).
Fries, Christian P.; Kienitz, Jörg: Monte-Carlo Simulation with Boundary Conditions (with Applications to Stress Testing, CEV and Variance-Gamma Simulation). 2010.
 The Monte-Carlo valuation (line) and its error estimate (corridor) for a European call option: Standard Monte-Carlo valuation (red), Monte-Carlo valuation with linear boundary condition (green) and analytic benchmark (blue).
The Monte-Carlo valuation (line) and its error estimate (corridor) for a European call option: Standard Monte-Carlo valuation (red), Monte-Carlo valuation with linear boundary condition (green) and analytic benchmark (blue).
In this paper we discuss how to incorporate analytic boundary conditions into a Monte-Carlo simulation framework and discuss their applications. The method introduced can dramatically improve the stability, robustness and accuracy of the valuation, calculation of sensitivities and stress testing, i.e., valuation under stressed model parameters.
We propose a Monte-Carlo simulation scheme which features boundary conditions for the underlying value process. The boundary conditions are analogous to the boundary conditions of a PDE. The Monte-Carlo simulation will then be modified to generate paths only within the boundaries and generate the corresponding Monte-Carlo weights. In addition, the valuation algorithm is adjusted to incorporate the analytic boundary conditions, using given or estimated boundary values for the value process.
The complete setup consists of four parts:
Part of this paper is presented at