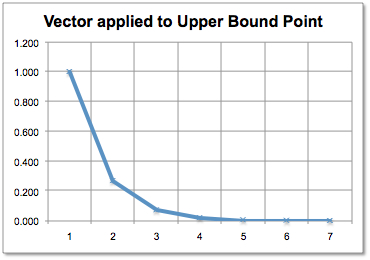
Left column of backward transition matrix.
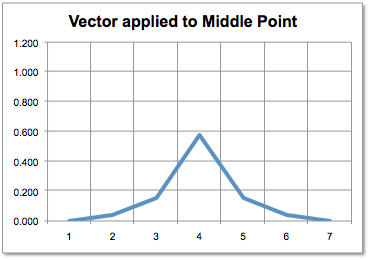
Middle column of backward transition matrix.
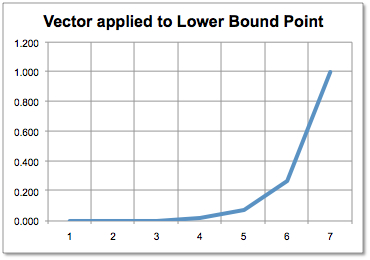
Right column of backward transition matrix.
On this page you find some additional material related to the paper
Fries, Christian P.: Stressed in Monte-Carlo. 2010.
The following movie depicts a Monte-Carlo simulation using a standard log-Euler scheme for a log normal process (which has, apparently no time-discretization error) to sample 100-paths. Due to the log-normal dampening all paths will tend to zero as volatility increases. While the effect is trivial to understand, it may come as a surprise if you apply large volatility shocks to your model.
|
Movie of 100 sample path of a log normal process for different volatilites. |
The following picture show columns of the backward transition matrix of an implicit Euler PDE scheme (very poor discretization).

Left column of backward transition matrix. |

Middle column of backward transition matrix. |

Right column of backward transition matrix. |
When volatility grows, the transition matrix converges to a simple linear interpolation. The effect is due to the boundary condition of the PDE.
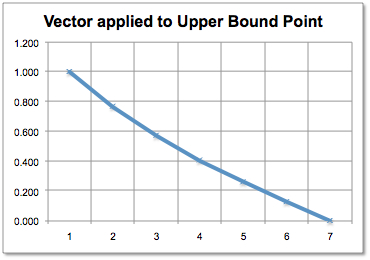
Left column of backward transition matrix. |
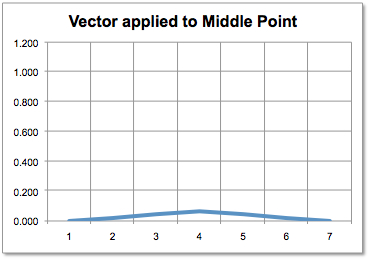
Middle column of backward transition matrix. |
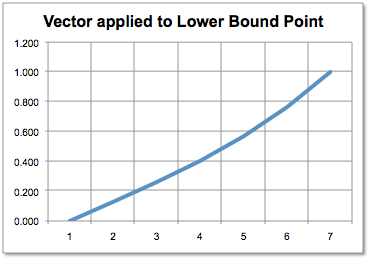
Right column of backward transition matrix. |
You may download the corresponding Excel Sheet.