Proxy Scheme Method

Contents

• Full Proxy Simulation Scheme Method (Fries / Kampen, 2005)
• Partial Proxy Simulation Scheme Method (Fries / Joshi, 2006)
• Localized Proxy Simulation Scheme Method (Fries, 2007)

(Full) Proxy Simulation Scheme Method

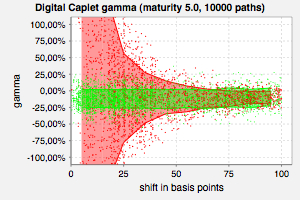
The gamma of a digital caplet evaluated by finite differences applied to standard Monte-Carlo simulation (red) and finite differences (!) applied to proxy scheme simulation (green). The error of the proxy scheme method exhibits no dependence on the shift size.

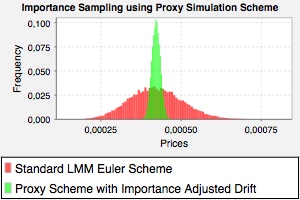
Monte-Carlo prices using a standard Euler-Scheme with the standard LIBOR Market Model drift (red) and a Proxy Simulation Scheme with an artificially adjusted drift (green). The drift of the proxy scheme has been increased such that the expectation of the forward rate falls into the region of the strike of the option.

Fries, Christian P.; Kampen, Jörg: Proxy Simulation Schemes for generic robust Monte-Carlo sensitivities, process oriented importance sampling and high accuracy drift approximation (with applications to the LIBOR Market Model). (PDF, 5.3 MB). (Version 1.2.1 - August 24th, 2006).

Download

• PDF, 5.3 MB

Abstract

We consider a generic framework for generating likelihood ratio weighted Monte Carlo simulation paths, where we use one simulation scheme K° (proxy scheme) to generate realizations and then reinterpret them as realizations of another scheme K* (target scheme) by adjusting measure (via likelihood ratio) to match the distribution of K* such that

This is done numerically in every time step, on every path.

This makes the approach independent of the product (the function f) and even of the model, it only depends on the numerical scheme.

The approach is essentially a numerical version of the likelihood ratio method [Broadie & Glasserman, 1996] and Malliavin's Calculus [Fournie et al., 1999; Malliavin, 1997] reconsidered on the level of the discrete numerical simulation scheme.
Since the numerical scheme represents a time discrete stochastic process sampled on a discrete probability space the essence of the method may be motivated without a deeper mathematical understanding of the time continuous theory (e.g. Malliavin's Calculus).

• high accuracy drift approximations,
• process oriented importance sampling and the
• robust calculation of partial derivatives of expectations w.r.t. model parameters (i.e. sensitivities, aka. Greeks) by applying finite differences by reevaluating the expectation with a model with shifted parameters.

We present numerical results using a Monte-Carlo simulation of the LIBOR Market Model for benchmarking.

Partial Proxy Simulation Scheme Method

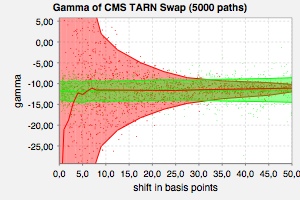
The gamma of a CMS target redemption note evaluated by finite differences applied to standard Monte-Carlo simulation (red) and finite differences (!) applied to a partial proxy scheme simulation (green). The error of the proxy scheme method exhibits no dependence on the shift size. The proxy constraint used ensured rigidity of the underlying CMS rate in a standard LIBOR market model.

Fries, Christian P.; Mark, Joshi S.: Partial Proxy Simulation Schemes for Generic and Robust Monte-Carlo Greeks. 2006. Version 1.1.0.

Download

Download form SSRN.

Abstract

We consider a generic framework which allows to calculate robust Monte-Carlo sensitivities seamlessly through simple finite difference approximation. The method proposed is a generalization and improvement of the proxy simulation scheme method (Fries and Kampen, 2005). As a benchmark we apply the method to the pricing of digital caplets and target redemption notes using LIBOR and CMS indices under a LIBOR Market Model. The framework is generic in the sense that it is model and almost product independent. The only product dependent part is the specification of the proxy constraint. This allows for an elegant implementation, where new products may be included at small additional costs.

Localized Proxy Simulation Scheme Method

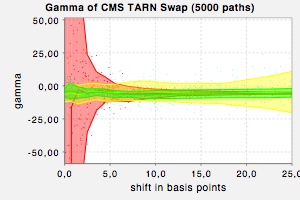
Gamma of a target redemption note (the coupon is a reverse CMS rate) calculated by finite difference applied to direct simulation (red), to a partial proxy scheme simulation (yellow) and to a localized proxy simulation scheme (green). Direct simulation produces enormous Monte-Carlo variances for small shift sizes. The partial proxy simulation scheme shows an increase in Monte-Carlo variance if the shift size is large. The localized proxy simulation scheme is an improvement on the partial proxy simulation scheme and shows only small Monte-Carlo variance for large shifts. Note: The localizer used is not the optimal one.

Fries, Christian P.: Localized Proxy Simulation Schemes for Generic and Robust Monte-Carlo Greeks. (2007)

Download

Download form SSRN.

Abstract

For the numerical calculation of partial derivatives (aka.~sensitivites or greeks) from a Monte-Carlo simulation there are essentially two possible approaches: The pathwise method and the likelihood ratio method. Both methods have their shortcomings: While the pathwise method works very well for smooth payouts it fails for discontinuous payouts. On the other hand, the likelihood ratio gives much better results on discontinuous payouts, but falls short of the pathwise method if smooth payouts are considered.

In this paper, we present a modification to the proxy simulation scheme framework, resulting in a per-path selection of either the pathwise method or the likelihood ratio method. This allows us to chose the optimal simulation method on a path-by-path basis.

Since the method is implemented as a proxy simulation scheme as well, the sensitivities can be calculated from simple finite differences applied to the pricing engine.

Other Resources

• Presentation: Proxy Simulation Schemes: Presented at Quantitative Methods in Finance - 14-17 December 2005 - Sydney, Australia.
• Presentation: Proxy Simulation Schemes: Presented at 3rd Fixed Income Conference - 21-22 September 2006 - Amsterdam, Netherlands.

More Numerical Results

I will post more numerical results here soon.