Fast and Robust Monte Carlo CDO Sensitivities

Rott, Marius G.; Fries, Christian P.: Fast and Robust Monte Carlo CDO Sensitivities and their Efficient Object Oriented Implementation. Version 0.9.2. May 31, 2005. [602 KB] - Download from DefaultRisk.com.

Abstract

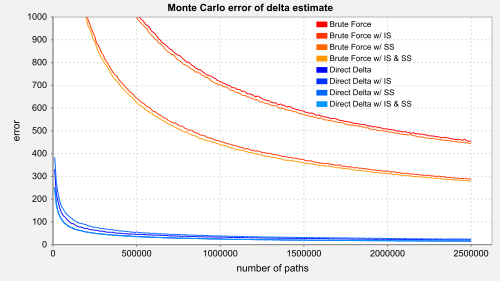
Convergence rate of CDO delta for standard finite differences (aka. brute force) with different variance reduction techniques [red] and the method using the conditional cumulative default time distribution (aka. direct delta) [blue].

In this paper we present a simple yet generic method for fast and robust Monte-Carlo calculation of sensitivities of Collateralized Debt Obligations (CDOs). The method is product independent and only relies on four pricings against modified models. From a modeling perspective the method is also fairly general as it only relies on the availability of a conditional cumulative distribution function for the default time. In our presentation we concentrate on conditional independent loss models as given in [Li2000].

The method we propose in this paper is generic and allows for an equally generic object oriented implementation which is highly efficient with respect to calculation performance and coding time (time to market). We present the design pattern of a stochastic iterator, the default time iterator, to create a highly flexible product implementation framework in which any product may become the underlying of any other product. Our benchmark calculations indicate that our method improves calculation time by a factor of around 1000 compared to brute force finite differences. The coding of a new product still remains on a "plug-and-play" level with very short development time.

JEL Class: C63, G13

Comments and suggestions welcomed at email@christian-fries.de.