Foresight Bias and Suboptimality Correction in Monte-Carlo Pricing of Options with Early Exercise: Classification, Calculation and Removal
Fries, Christian P.: Foresight Bias and Suboptimality Correction in Monte-Carlo Pricing
of Options with Early Exercise: Classification, Calculation and Removal. Version 1.1.4. November 28, 2005. [3.0 MB]. This paper is available at SSRN.
Contents
| 1 | Introduction | 3 |
| 1.1 | Plan of the Paper | 3 |
| 2 | Bermudan Options: Notation | 4 |
| 2.1 | Relative Prices | 4 |
| 2.2 | Bermudan Option as Optimal Exercise Problem | 4 |
| 2.3 | Bermudan Option Value as single (unconditioned) Expectation: The Optimal Exercise Value | 4 |
| 3 | The Backward Algorithm | 5 |
| | Induction start: | 5 |
| | Induction step | 5 |
| 4 | Conditional Expectation Estimators | 6 |
| 4.1 | Conditional Expectation as Functional Dependence | 6 |
| 4.2 | Perfect Foresight | 6 |
| 4.3 | Binning | 6 |
| 4.4 | Regression Methods - Least Square Approximation of the Conditional Expectation | 7 |
| 4.4.1 | Example: Evaluation of an Bermudan Option on a Stock (Backward Algorithm with Conditional Expectation Estimator) | 9 |
| | Induction start: $t > T_{n}$ | 9 |
| | Induction step: $t = T_{i}$, $i = n, n-1, n-2, \ldots 1$ | 9 |
| 5 | Foresight Bias: Classification, Calculation \& Removal | 10 |
| 5.1 | Numerical Removal of the Foresight Bias | 10 |
| 5.2 | Motivation for an Analytical Estimate and Removal of Foresight Bias | 10 |
| 5.3 | Estimation of the Foresight Bias | 10 |
| 5.4 | Analytical Removal of Foresight Bias | 12 |
| 5.5 | Analytical Removal of Foresight Bias and Suboptimal Exercise | 13 |
| 5.6 | Implementation of the Analytical Removal of Foresight Bias | 14 |
| 5.6.1 | Calculation of the Monte-Carlo error | 14 |
| | Binning: | 14 |
| | Regression: | 14 |
| 5.7 | Is the foresight bias negligible? | 15 |
| 5.7.1 | Aggregating Foresight Biased Options | 15 |
| 5.7.2 | Parallelization of Pricing with Foresight Bias | 15 |
| 6 | Numerical Results | 16 |
| 6.1 | Benchmark Model | 16 |
| 6.2 | Aggregation of Monte-Carlo Prices | 16 |
| 6.3 | Relation of Foresight Bias to Monte-Carlo Error | 19 |
| 6.3.1 | Example 1: Bermudan Option with three Exercise Dates | 19 |
| 6.3.2 | Example 2: Bermudan Option with nine Exercise Dates | 20 |
| 6.3.3 | Example 3: A Portfolio of Bermudan Options | 22 |
| 7 | Conclusion | 25 |
| | List of Symbols | 26 |
| | References | 27 |
| | Notes | 27 |
Download
Abstract
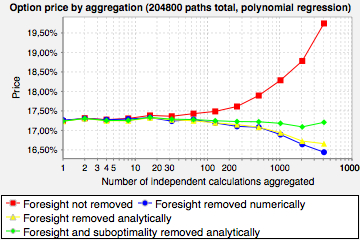
Monte Carlo price for different levels of aggregation. Starting with a single Monte Carlo simulation with 2048000 paths we price the same option with two, four, eight, etc. smaller simulations and average the prices. Foresight bias becomes a strong effect when aggregating prices from many simulations with a small number of paths (5000 or less). Our corrections improve the prices even if a extremly small number of paths (50) is used.
In this paper we investigate the so called foresight bias that may appear in the Monte-Carlo pricing of Bermudan and compound options if the exercise criteria is calculated by the same Monte-Carlo simulation as the exercise values. The standard approach to remove the foresight bias is to use two independent Monte-Carlo simulations: One simulation is used to estimate the exercise criteria (as a function of some state variable), the other is used to calculate the exercise price based on this exercise criteria. We shall call this the numerical removal of the foresight bias.
In this paper we give an exact definition of the foresight bias in closed form and show how to apply an analytical correction for the foresight bias.
Our numerical results show that the analytical removal of the foresight bias gives similar results as the standard numerical removal of the foresight bias. The analytical correction allows for a simpler coding and faster pricing, compared to a numerical removal of the foresight bias.
Our analysis may also be used as an indication of when to neglect the foresight bias removal altogether. While this is sometimes possible, neglecting foresight bias will break the possibility of parallelization of Monte-Carlo simulation and may be inadequate for Bermudan options with many exercise dates (for which the foresight bias may become a Bermudan option on the Monte-Carlo error) or for portfolios of Bermudan options (for which the foresight bias grows faster than the Monte-Carlo error).
In addition to an analytical removal of the foresight bias we derive an analytical correction for the suboptimal exercise due to the uncertainty induced by the Monte-Carlo error. The combined correction for foresight bias (biased high) and suboptimal exercise (biased low) removed the systematic bias even for Monte-Carlo simulations with very small number of paths.
Acknowledgement
I would like to thank Markus Meister for his interest in an early version of this paper and a very stimulating discussion as well as for his constructive comments to this and my other works. I thank Oliver Dauben for his continuous advisory with respect to Java™ technology. I am grateful to Rosemarie Philippi for her support.
Interactive Experiment
You may explore the analytical and numerical removal of foresight bias in the Java applet for Bermudan (equity) option pricing.
Classification
- MSC-class: 65C05 (Primary), 68U20, 60H35 (Secondary).
- ACM-class: G.3; I.6.8.
- JEL-class: C15, G13.
- Keywords: Early Exercise, Bermudan Options, Compound Options, Monte-Carlo, Foresight
Comments and suggestions welcomed at email@christian-fries.de.

