Monte-Carlo Methods on GPGPU with Applications to Mathematical Finance
There will be a workshop on
Monte-Carlo Methods on GPGPU with Applications to Mathematical Finance
at the LMU quantLab. For details see http://www.fm.mathematik.uni-muenchen.de/news/gpu_workshop_news/index.html
Implementation of the YEARFRAC function in Excel (2013), LibreOffice (4.1) and OpenOffice (4.0)
Setting up a demo spreadsheet for a workshop, I - accidentally - found my self comparing the calculation of day count fractions using finmath lib's Java implementation with the calculation using the spreadsheets YEARFRAC function.
To my surprise, the implementation of this function is surprisingly unclear and inconsistent.
Some facts about YEARFRAC in Excel, LibreOffice, OpenOffice.
The spreadsheet function YEARFRAC(Date start, Date end, Integer basis) implement five different methods for calculating day count fractions, depending on the value of basis = 0, 1, 2, 3, 4. According to the "documentation" these methods are 30U/360 (basis=0), ACT/ACT (basis=1), ACT/360 (basis=2), ACT/365 (basis=3), 30E/360.
- The Excel implementation of "ACT/ACT", i.e. YEARFRAC(start, end,4) does not agree with - the very common - ACT/ACT ISDA. I saw a claim that Excel implements ACT/ACT AFB, but I could not verify this claim.
- I have a reimplementation of all 4 daycount
conventions implemented by Excel. These are
available in
finmath lib. They are:
- For 30U/360 (basis=0) see DayCountConvention_30U_360.java
- For ACT/ACT (basis=1) see DayCountConvention_ACT_ACT_YEARFRAC.java
- For ACT/360 (basis=2) see DayCountConvention_ACT_360.java
- For ACT/365 (basis=3) see DayCountConvention_ACT_365.java
- For 30E/360 (basis=4) see DayCountConvention_30E_360.java
- The implementation of Excel ACT/ACT does not agree with ACT/ACT ISDA, which you can find at DayCountConvention_ACT_ACT_ISDA.java
- The implementation of Excel ACT/ACT does not agree with ACT/ACT AFB which you can find at DayCountConvention_ACT_ACT_AFB.java
- The implementation of Excel ACT/ACT and LibreOffice ACT/ACT do not agree, although it agrees in many cases. In some cases the values are off by a factor of 365/366, i.e., 0,3%
- The implementation of LibreOffice ACT/ACT (i.e. YEARFRAC with basis=1) differs from the implementation in Excel (a bug report has been filed to the LibreOffice group).
- The implementation of OpenOffice ACT/ACT differs from the implementation in Excel and from the implementation in LibreOffice (a bug report has been filed to the OpenOffice group)
The implementation of YEARFRAC ACT/ACT does not make sense from a financial point of view.
Since the YEARFRAC may be interpreted as accrual factors for interest rate periods we may consider a few desirable properties. Surprisingly Excel fails in many trivial requirements:
Property 1: Additivity. The yearfrac should be additive. For Excel this is not the case: YEARFRAC(30.12.2011, 04.01.2012, 1) is not equal to YEARFRAC(30.12.2011, 01.01.2012, 1) + YEARFRAC(01.01.2012, 04.01.2012, 1).
Property 2: Proportional Leap Year Attribution. Assume that 8 quaterly periods span exactly two years (DD.MM.YYYY to DD.MM.(YYYY+2) and assume that YYYY+1 is a leap year. Since the numerator of act/act measures actual days, we expect that the denominator will have 4 times 365 and 4 times 366. For Excel and LibreOfffice this is not the case. In Excel only 3 of the 8 Periods 01.07.99, 01.10.99, 01.01.00, 01.04.00, 01.07.00, 01.10.00, 01.01.01, 01.04.01, 01.07.01 receive a denominator of 366. In LibreOffice (4.1) 5 of the 8 Periods get a denominator of 366.
Note: ACT/ACT ISDA fulfills both properties.
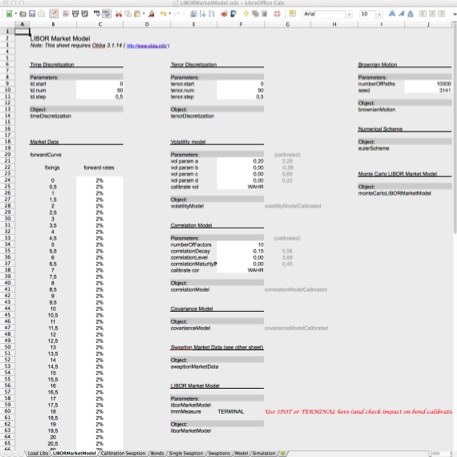
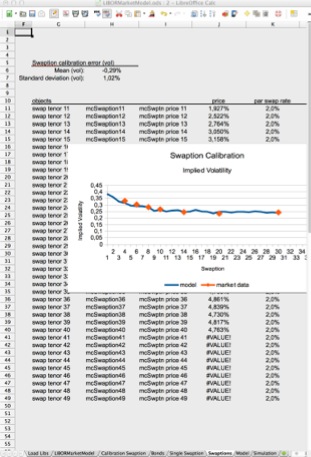
LIBOR Market Model: Spreadsheet and Source Code
Spreadsheet and code for the LIBOR market model added to finmath.net. Java source code availabe from the finmath lib subversion repository.
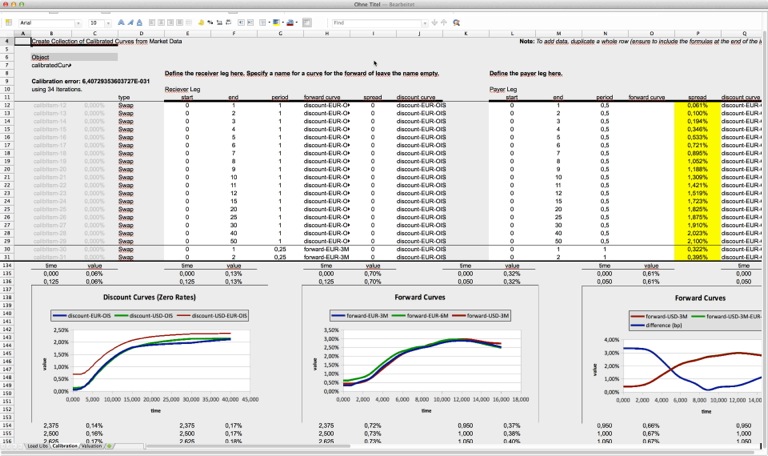
Curve Calibration: Spreadsheet and Source Code
Demo spreadsheet for the calibration of curves (discount curves, forward curves) to interest rate swaps added to the spreadsheets section of finmath.net. Java source code availabe from the finmath lib subversion repository.
Vorlesung 2012/2013: Numerische Methoden der Finanzmathematik
- Numerische Methoden der Finanzmathematik.
finden sich unter http://www.christian-fries.de/finmath/lecture12-13/.
Vorlesung 2012: Finanzmathematik: Bewertungsmethoden für Zinsderivate. Vor und nach der Finanzkrise.
- Finanzmathematik: Theorie, Modellierung und
objektorientierte Implementierung von
Bewertungsmethoden für Zinsderivate.
Vor und nach der Finanzkrise.
findet sich unter http://www.christian-fries.de/finmath/lecture12/.