Research (English Text)
Christian Fries' Blog

Conditional Analytic Monte-Carlo Pricing Scheme for Auto-Callables

27. 04 08 - 23:43 -
We renamed the paper cited in the Journal of Computational Finance 11(3) as "A semi-analytic Monte Carlo pricing scheme for auto-callable products". Its new title is "Conditional Analytic Monte Carlo Pricing Scheme for Auto-Callable Products".

Tags:

Partial Proxy Simulation Schemes for Robust Monte-Carlo Sensitivities

30. 09 06 - 23:33 -
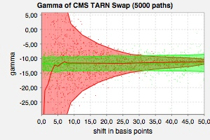
CMS_TARN_Swap_Gamma_vs_Shift_-_numberOfPath_5000_maxShift_50
We consider a generic framework which allows to calculate robust Monte-Carlo sensitivities seamlessly through simple finite difference approximation. The method proposed is a generalization and improvement of the proxy simulation scheme method (Fries and Kampen, 2005).

As a benchmark we apply the method to the pricing of digital caplets and target redemption notes using LIBOR and CMS indices under a LIBOR Market Model. We calculate stable deltas, gammas and vegas by applying direct finite difference to the proxy simulation scheme pricing.

The framework is generic in the sense that it is model and almost product independent. The only product dependent part is the specification of the proxy constraint. This allows for an elegant implementation, where new products may be included at small additional costs.

For more information see http://www.christian-fries.de/finmath/proxyscheme.

Equity Markov Functional Model

02. 04 06 - 10:24 -
MarkovFunctionalLIBORCalibration
I wrote a small note on how to do Markov Functional Modeling for a single asset (like equity). The "trick" only works if you use the asset itself as Numéraire. However, on the other hand, this is exactly what you do in Markov Functional Modeling of interest rates, where the Numéraire is an interest rate product. The approach in this note is very similar to the Markov Functional Model in spot LIBOR measure (the original Makov Functional Model was specified in terminal measure).
Version 0.4 of the paper is still lacking an introduction.

(Edit 14.04.06): In Version 0.8 I have added a nice discussion on model dynamics, using Black-Scholes like functionals as a starting point for my examples. The discussion shows how to calibrate the joint asset-interest rate dynamics (ie. r(S)) and forward volatility (all this in addition to the calibration to a full two dimensional smile surface.